(Peer-Reviewed) SSP IMEX Runge-Kutta WENO Scheme for Generalized Rosenau-KdV-RLW Equation
Muyassar Ahmat, Jianxian Qiu 邱建贤
School of Mathematical Sciences and Fujian Provincial Key Laboratory of Mathematical Modeling and High-Performance Scientific Computing, Xiamen University, Xiamen 361005, China
中国 厦门 厦门大学数学科学学院 福建省数学建模与高性能科学计算重点实验室
Abstract
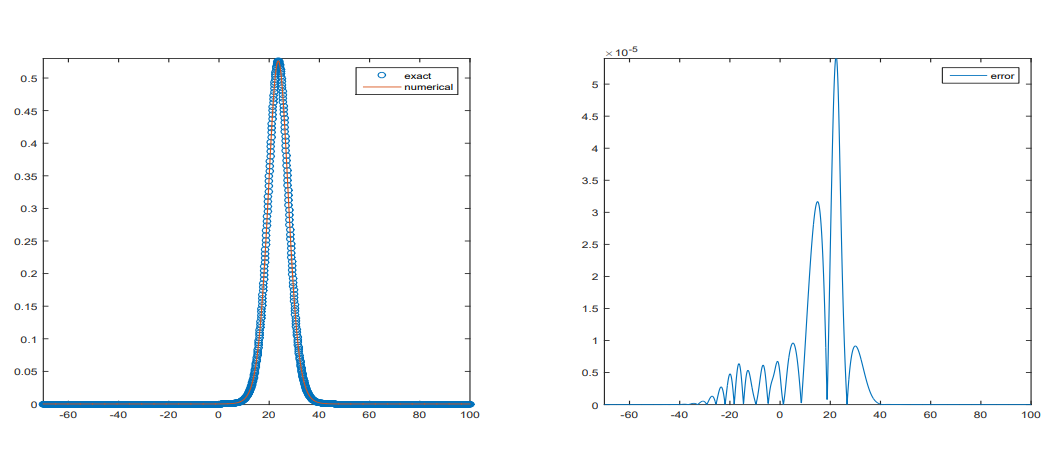
In this article, we present a third-order weighted essentially non-oscillatory (WENO) method for generalized Rosenau-KdV-RLW equation. The third order finite difference WENO reconstruction and central finite differences are applied to discrete advection terms and other terms, respectively, in spatial discretization.
In order to achieve the third order accuracy both in space and time, four stage third-order L-stable SSP Implicit-Explicit Runge-Kutta method (Third-order SSP EXRK method and thirdorder DIRK method) is applied to temporal discretization. The high order accuracy and essentially non-oscillatory property of finite difference WENO reconstruction are shown for solitary wave and shock wave for Rosenau-KdV and Rosenau-KdV-RLW equations.
The efficiency, reliability and excellent SSP property of the numerical scheme are demonstrated by several numerical experiments with large CFL number.
Flicker minimization in power-saving displays enabled by measurement of difference in flexoelectric coefficients and displacement-current in positive dielectric anisotropy liquid crystals
Junho Jung, HaYoung Jung, GyuRi Choi, HanByeol Park, Sun-Mi Park, Ki-Sun Kwon, Heui-Seok Jin, Dong-Jin Lee, Hoon Jeong, JeongKi Park, Byeong Koo Kim, Seung Hee Lee, MinSu Kim
Opto-Electronic Advances
2025-09-25
Dual-frequency angular-multiplexed fringe projection profilometry with deep learning: breaking hardware limits for ultra-high-speed 3D imaging
Wenwu Chen, Yifan Liu, Shijie Feng, Wei Yin, Jiaming Qian, Yixuan Li, Hang Zhang, Maciej Trusiak, Malgorzata Kujawinska, Qian Chen, Chao Zuo
Opto-Electronic Advances
2025-09-25